«●—【前言】—●○»
简单的氢原子对量子理论的发展产生了很大的影响,特别是在20世纪上半叶,量子力学的基础已经奠定。
随着测量技术的改进,在氢的光谱中解决了更精细的细节,直到最终观察到谱线的分裂,这甚至不能用量子力学的完全相对论性公式来解释,但需要更先进的量子电动力学理论。
我们之前研究了氢的玻尔-索姆菲尔德的理论,该理论经典地处理电子轨道,并对它们施加量子化规则。
这一理论解释了氢的许多特征,但它不能提供对具有一个以上电子的系统的现实描述,例如氦原子。

虽然电子绕原子核运行的简单图像,就像围绕太阳的行星一样,可以解释一些现象,但它已经被薛定谔方程和波函数所取代。
我们现在来概述一下这种方法在求解氢原子的施¨方程中的应用;这导致了与玻尔模型相同的能级,但波函数提供了更多的信息,例如,它们允许计算能级之间的跃迁速率。
同时我们展示一下由相对论效应引起的扰动如何导致精细结构。
«●—【薛定谔方程】—●○»
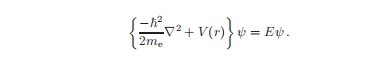
这是总能量守恒的经典方程的量子力学对应物,表示为动能和势能的总和。

运算符l2包含依赖于θ和φ的项,即
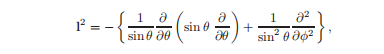
按照求解偏微分方程的通常程序,我们寻找一个以函数ψ = R (r)Y(θ,φ)的乘积形式存在的解。公式分为径向和角部分如下:
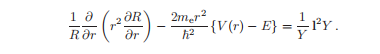
每一边都依赖于不同的变量,所以只有当两边都等于一个我们称为b的常数时,方程才被满足。
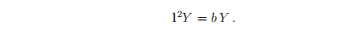
这是一个本征值方程,我们将使用角动量算子的量子理论来确定本征函数Y(θ,φ)。
«●—【角方程的解】—●○»
为了继续分离变量,我们将Y = Θ(θ)Φ(φ)替换为上述公式,得到:
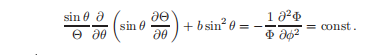
Φ(φ)的方程与简谐运动相同,所以:
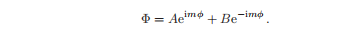
上述右边的常数的值为m2,物理上真实的波函数在每个点上都有一个唯一的值,这就施加了条件Φ(φ + 2π)= Φ(φ),所以m必须是一个整数。
函数Φ(φ)是轨道角动量的z分量的算子的特征函数的和。
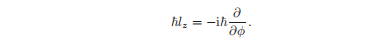
函数eimφ的磁量子数为m,其复共轭e−imφ的磁量子数为−m。
找到函数Y(θ,φ)及其特征值−的一个方便方法是使用l+ = lx + ily和 l− = lx − ily。
这些算子与l2交换,总角动量平方的算子(因为lx和ly与l2交换);因此,三个函数Y、l+Y和−都是l2的特征函数,具有相同的特征值−(如果它们非零,如下所述)。
阶梯运算符可以用极坐标表示为:
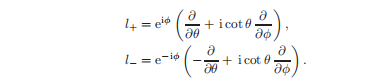
算子l+将一个磁量子数为m的函数转换为另一个特征值为m + 1的角动量本征函数,因此,l+被称为提升操作符。6降低算符l−在另一个方向上改变磁量子数,m→m−1。
可以证明这些语句和这些操作符的其他性质。
重复应用提升算符不会无限地增加m——对于每个特征值b,都有一个磁量子数的最大值,我们将称之为l,即mmax = l。
作用于具有mmax的特征函数的算子给出了零,因为根据定义没有具有m>mmax的特征函数。因此,通过求解方程l+Y=0,我们发现具有mmax = l的特征函数具有这样的形式。
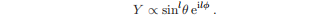
这些是特征值b = l(l + 1)的特征函数l2),l是轨道角动量量子数。函数Yl、m(θ、φ)用传统的特征值进行标记。
对于l = 0,只有m = 0存在,Y0,0是一个常数,没有角依赖性。
对于l = 1,我们可以从l=1=m(eqn2.10)开始,并使用降低算子找到其他特征函数:
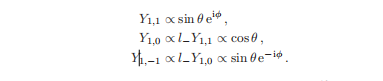
这给出了l = 1的所有三个特征函数。
对于l = 2,这个程序给出:
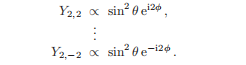
这是m=2,1,0,−1,−2的五个特征函数。
轨道角动量本征函数表

要理解原子的性质,了解波函数是什么样子是很重要的。
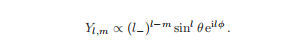
角分布需要乘以在下一节中计算出的径向分布,才能得到波函数的平方为:
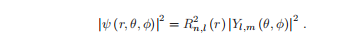
这是电子的概率分布,或−e|ψ|2可以解释为电子电荷分布。
然而,许多原子的性质主要取决于角分布和图的形式。
这些分布与电子绕z轴的圆周运动之间存在对应关系,我们在经典的塞曼效应理论中发现了正规模态。
量子力学中的静止态对应于时间平均的经典运动。在这种情况下,围绕x轴的两个圆周运动方向是相同的分布。

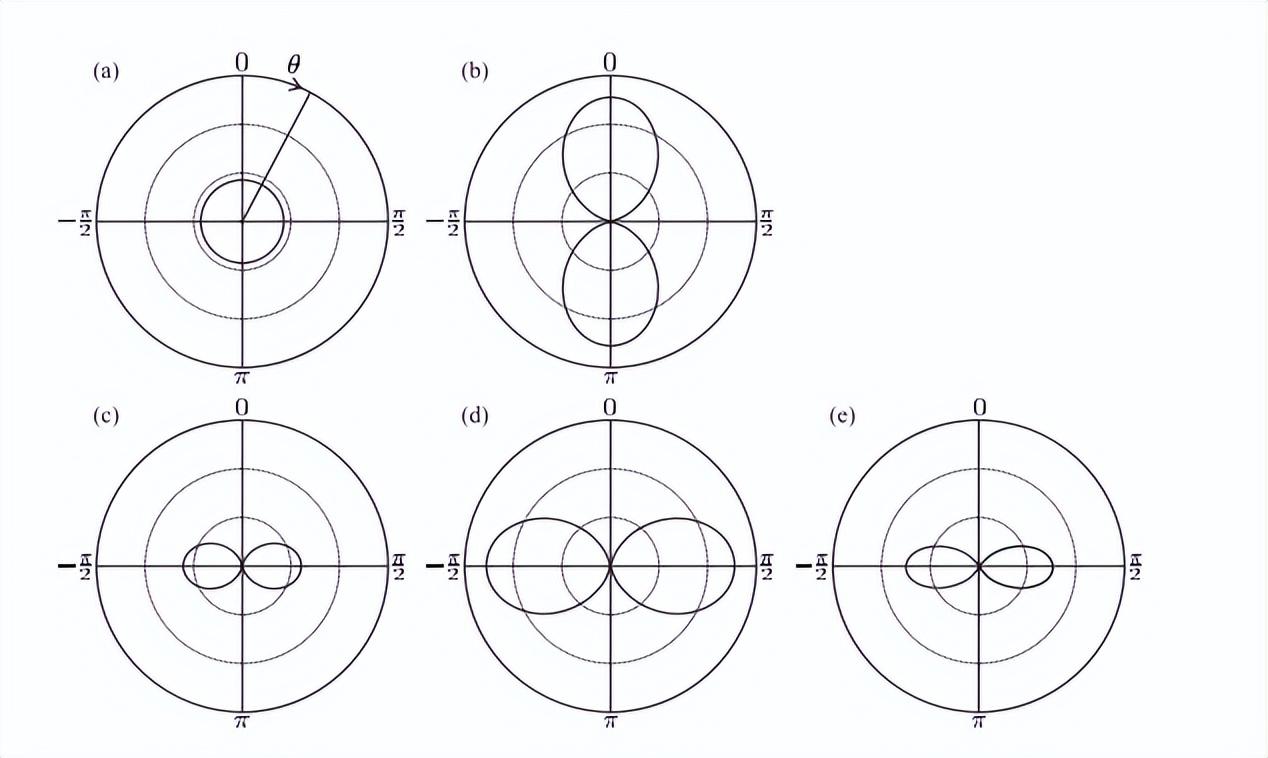
它们的任何线性组合也是l2的特征函数。
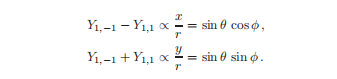
这两个实函数的形状与Y1相同,分别为0∝z/r,但分别沿着x轴和y轴对齐。
在没有外场打破球面对称的情况下,所有的轴都是等价的,即原子没有一个首选的方向,所以在x、y和z方向之间存在对称性。
在外加磁场中,不同值m(但值相同l)的状态不是简并的,因此它们的线性组合不是系统的本征态。

在化学方面对l=1的贡献被称为p-轨道。
计算机程序可以从任何期望的观看角度生成这些函数的图,这有助于用l > 1可视化函数(对于l = 0和1,在一个包含对称轴的平面上,一个函数的横截面就足够了)。
«●—【径向方程的解】—●○»
将以下设为常数b = l(l + 1),并加入库仑势V (r) =−e2 /4π0r,得到R (r)的方程。
可以通过替换P (r) = rR (r)铸造成方便的形式:
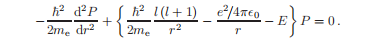
与l(l + 1)/r2成正比的项是与角自由度相关的动能;在这个径向方程中,它是一个有效势,倾向于使L不等于0的波函数远离原点。
将这个方程除以E=−|E|,并进行替换。
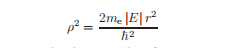
将方程简化为无量纲形式:
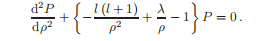
描述库仑相互作用强度的常数为:
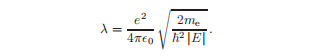
求解这种微分方程的标准方法是寻找一个级数形式的解。
级数解有有限数量的项,当λ = 2n时不发散,其中n是一个整数。
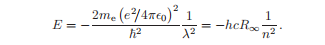
这表明在玻尔公式给出的能量下,Schr¨odinger方程具有平稳解。
能量不依赖于l;具有不同l的波函数的偶然简并度是库仑势的一个特殊特征。
相比之下,关于磁量子数ml的简并度是由于系统的对称性引起的,即在没有外部场的情况下,原子的性质与它在空间中的方向无关。
Schr¨odinger方程的解提供的信息不仅仅是能量,从波函数中,我们可以以波尔-索姆菲尔德理论中不可能的方式计算其他原子性质。

虽然能量只依赖于n,但波函数的形状同时取决于n和l,这两个量子数被用来标记径向函数Rn,l (r)。对于n = 1,只有l = 0溶液,即R1,0∝e−ρ。对于n = 2,轨道角动量量子数为l = 0或1,给出:
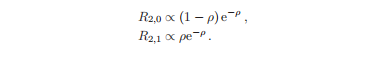
径向生水波函数Rn,l的变量ρ = Zr/(na0),它给出了一个随n变化的缩放。

这些表明了水波函数的一个一般特征,即l = 0的径向函数在原点有一个有限的值,即ρ中的幂级数从零次幂开始。
因此,具有l = 0的电子(称为s-电子)在原子核位置被发现的概率是有限的,这在原子物理学中具有重要的影响。
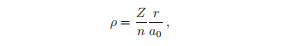
其中原子序数已由替换的e2 /4π0 → Ze2 /4π0 合并。
径向波函数有一些重要的性质,需要解的一般形式,我们陈述这些结果以供将来参考。原点为0的电子的概率密度为:
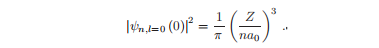
对于l不等于0的电子,期望值为1/r3。
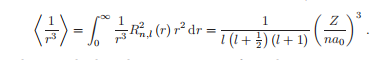
这些结果都是以一种很容易记住的形式写成的;它们必须都依赖于1/a3 0才能获得正确的维度,对主量子数n的依赖性似乎也来自于上述,但这是一个巧合。
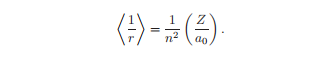
特定能量的Schr¨odinger方程的波函数解是驻波,并给出了电子电荷−e|ψ(r)|2的分布。
我们现在将考虑,当原子与产生振荡电场的电磁辐射相互作用时,这些稳态之间的跃迁是如何发生的。
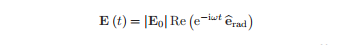
振幅|E0|和偏振矢量。如果ω位于t);在接近原子共振频率时,扰动电场使原子进入不同状态的叠加,并在原子上产生一个振荡的电偶极矩。
受激跃迁速率的计算需要时间依赖的微扰理论(TDPT)。
然而,从第一性原理开始进行的处理是漫长的,我们将预测一些结果,以便我们可以看到光谱是如何与原子能级的底层结构相关的。
这并不需要精确的跃迁速率计算,但我们只需要确定跃迁速率是否有一个有限的值或它是否为零(到一阶),即跃迁是允许的,并给出一个强谱线,还是禁止的。
含时变微扰理论的结果被封装在黄金法则(或费米黄金法则)中;这表明跃迁的速率与扰动的矩阵元素的平方成正比。
描述上图中与场的时变相互作用的哈密顿量为H=·E (t),其中电偶极子算子为−。这种与辐射的相互作用以一种速率刺激了从状态1到状态2的转变。
当辐射频率ω,与跃迁频率ω12相匹配时,请注意,我们将不讨论黄金规则中所谓的“态密度”,因为这对于单色辐射来说并不简单。
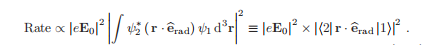
狄拉克表示法中的简明表达式便于以后使用,这种处理假设电场的振幅在原子上是均匀的,因此它可以在原子波函数的积分之外取,即e0不依赖于r.24我们把偶极子矩阵元素写成乘积。
波的相位实际上是(ωt−k·r),其中r是相对于原子质心的坐标(作为原点),k是波矢量。
我们假设相位k·r在原子(ka0 2π)上的变化很小,这相当于λ a0,即辐射的波长远远大于原子的大小。这叫做偶极子近似。

径向积分为:
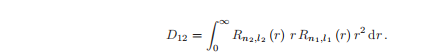
角积分为:
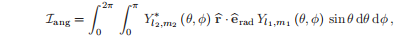
其中,r = r/r,径向积分通常不是零,尽管对于径向波函数有一个小重叠的状态之间的过渡,它可以很小,例如当n1很小,n2很大(或相反)。
«●—【总结】—●○»
相比之下,Iang = 0,除非满足严格的标准——这些是选择规则。
控制允许跃迁的选择规则来自于上述中的角积分,它包含了对给定辐射极化的相互作用r·erad的角依赖性。
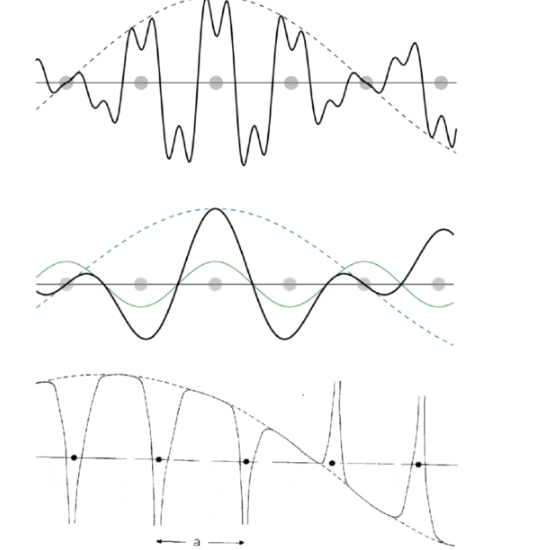
这与经历外部磁场塞曼效应的原子的物理情况相对应,将电子作为经典振荡器的处理表明,塞曼模式中不同频率的分量具有不同的极化。
我们在这里使用相同的π和σ跃迁命名法;横向观测指的是垂直于磁场发出的辐射,纵向观测是沿z轴进行的。
数学要求我们计算一个原子具有定义明确的量子化轴(总是选择为z轴)和具有定义明确的极化和传播方向的辐射的Iang。