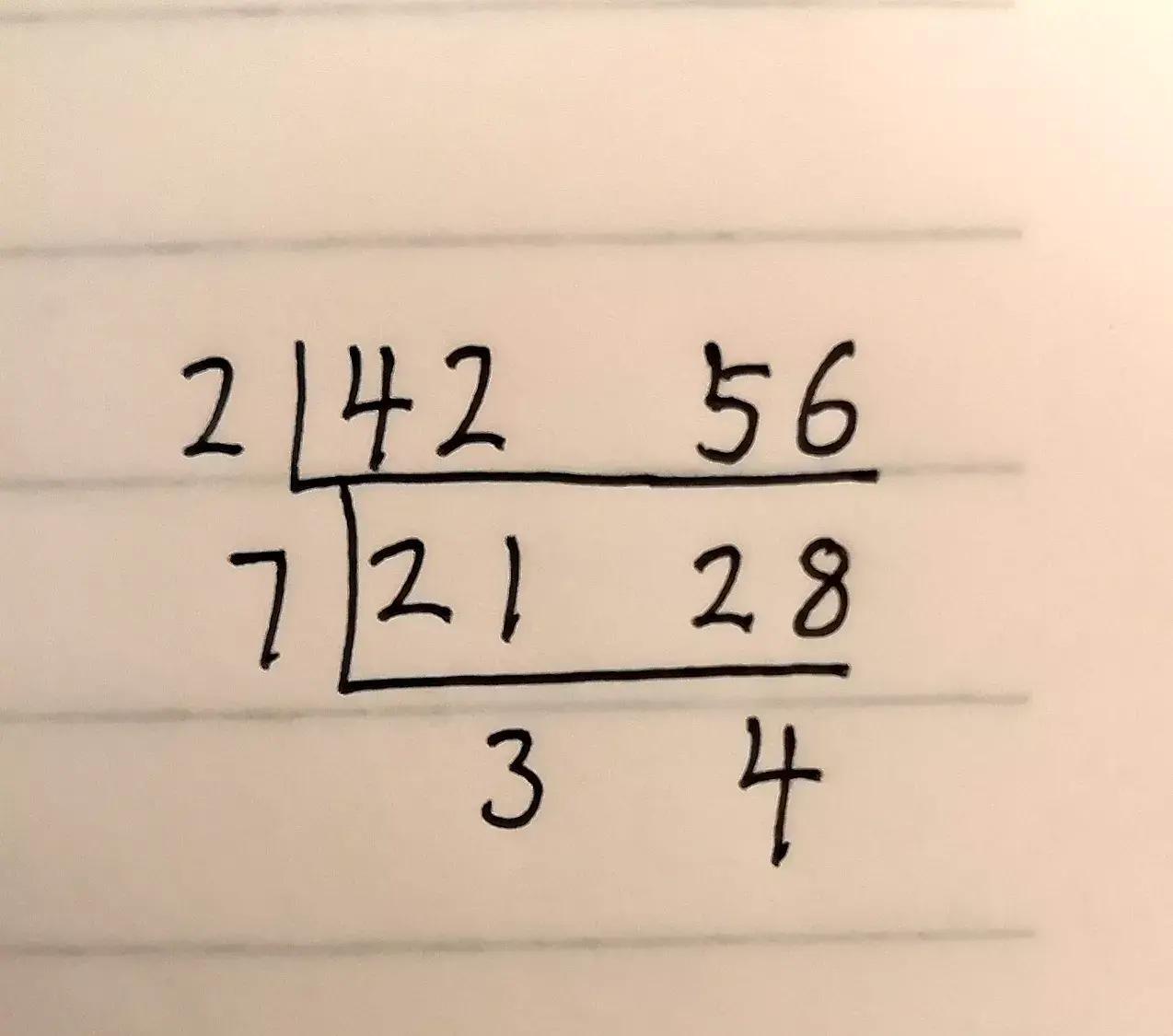可以分三类,逐次判断,采用对应方法。
一、存在倍数关系。大数÷小数,能整除。大数是这两个数的最小公倍数,小数是这两个数的最大公因数。
例如:24和12 24÷12=2,能整除。24是24和12的最小公倍数,12是24和12的最大公因数。
二、存在互质关系。公因数只有1的两个非零自然数称为互质数。两个数的乘积,是它们的最小公倍数。1,是它们的最大公因数。
例如:3和14 3和14的公因数只有1,所以3和14互质。3和14的乘积42,是3和14的最小公倍数。1,是3和14的最大公因数。
三、短除法。不属于上面两类的,可以用短除法去求最小公倍数和最大公因数。
方法:两个数同时除以质数,一般从最小的质数试起,都能整除的质数当除数;除到商互质为止;除数的连乘积就是这两个数的最大公因数。除数和商的连乘级就是这两个数的最小公倍数。
例如:18和56,先除以最小质数2,都可以整除,商分别是9、28,这时商9和28互质,不用继续除了。除数2就是18和56的最大公因数。除数2、商9、商28的连乘积就是18和56的最小公倍数。
2,是18和56的最大公因数。
2×9×28=504,是18和56的最小公倍数。
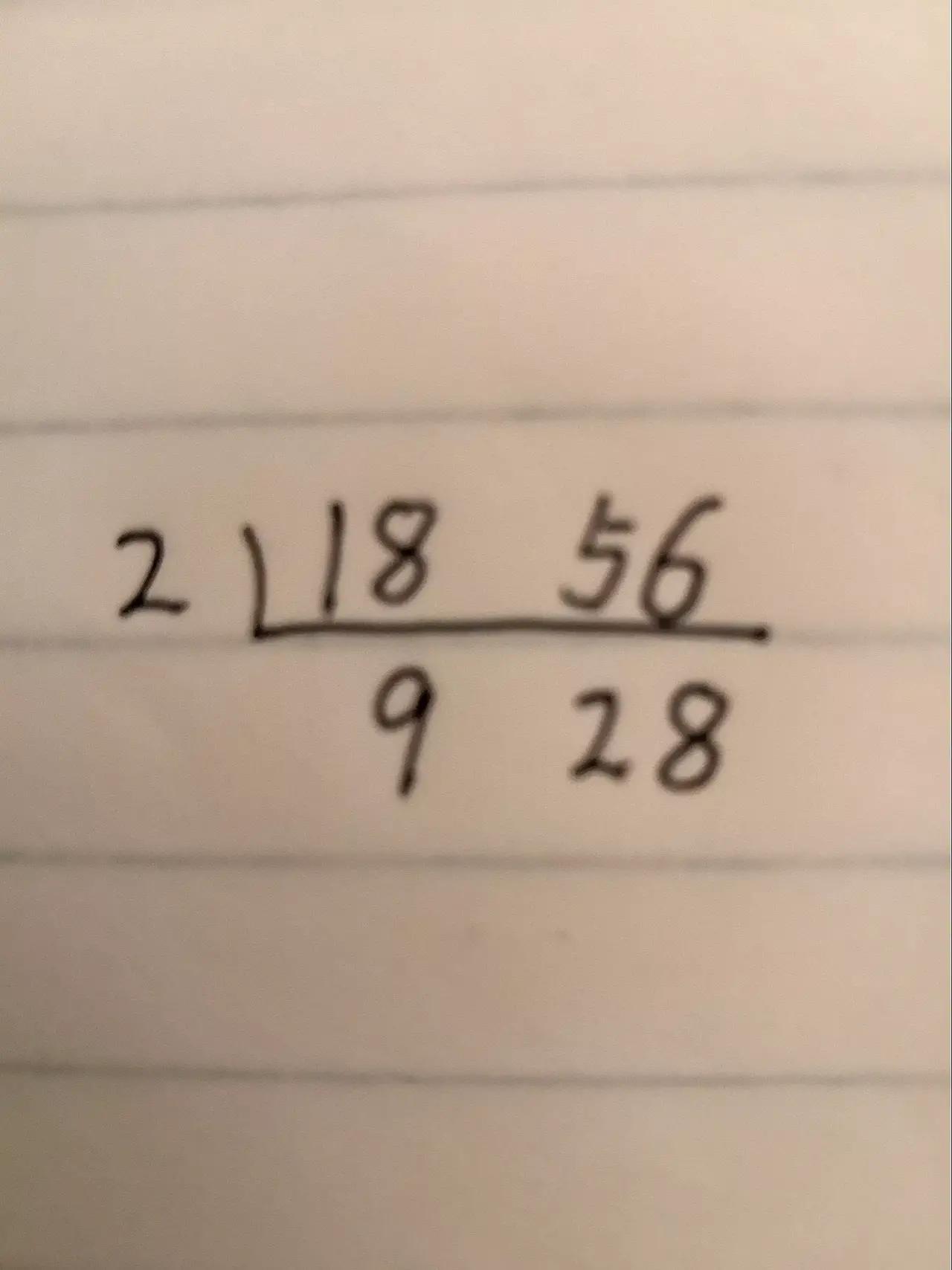
例如:42和56,先除以最小质数2,都能整除,商分别是21、28,但21和28不互质,要继续除。下一步,用商从除以最小质数开始,看看都能整除吗,2不行,3不行,5不行,继续换大点的质数,7可以。此时,商3和4互质,不用继续除了。
2×7=14,是42和56的最大公因数。
2×7×3×4=168,是42和56的最小公倍数。