指数平滑法是从移动平均法发展而来的,是一种改良的加权平均法,在不舍弃历史数据的前提下,对离预测期较近的历史数据给予较大的权数,权数由近到远按指数规律递减。
指数平滑法根据本期的实际值和预测值,并借助于平滑系数(α)进行加权平均计算,预测下一期的值。它是对时间序列数据给予加权平滑,从而获得其变化规律与趋势。
Excel中的指数平滑法需要使用阻尼系数(β),阻尼系数越小,近期实际值对预测结果的影响越大;反之,阻尼系数越大,近期实际值对预测结果的影响越小。
α——平滑系数(0≤α≤1)
β——阻尼系数(0≤β≤1),β=1-α
在实际应用中,阻尼系数是根据时间序列的变化特性来选取的。
★ 若时间序列数据的波动不大,比较平稳,则阻尼系数应取小一些,如0.1~0.3。
★ 若时间序列数据具有迅速且明显的变动倾向,则阻尼系数应取大一些,如0.6~0.9。
根据具体时间序列数据情况,我们可以大致确定阻尼系数(β)的取值范围,然后分别取几个值进行计算,比较不同值(阻尼系数)下的预测标准误差,选取预测标准误差较小的那个预测结果即可。
指数平滑法公式如下:
Yt = αXt-1+(1-α) Yt-1 = ( 1-β) Xt-1+βYt-1
式中,Yt ——时间t的平滑值;
Xt-1 ——时间t-1的实际值;
Yt-1——时间t-1的平滑值;
α ——平滑系数;
β ——阻尼系数。
指数平滑法可以分为一次指数平滑法、二次指数平滑法及三次指数平滑法,这里我们主要介绍一次指数平滑法。
以“企业季度数据”为例,利用Excel分析工具库——“指数平滑”分析工具预测2012年第3季度的销售额会是多少。
STEP 01 单击【数据】选项卡【分析】组中的【数据分析】按钮,在弹出的【数据分析】对话框中,选择【指数平滑】,单击【确定】按钮。
STEP 02 在弹出的【指数平滑】对话框中,各类参数分别进行如下设置,如图所示。
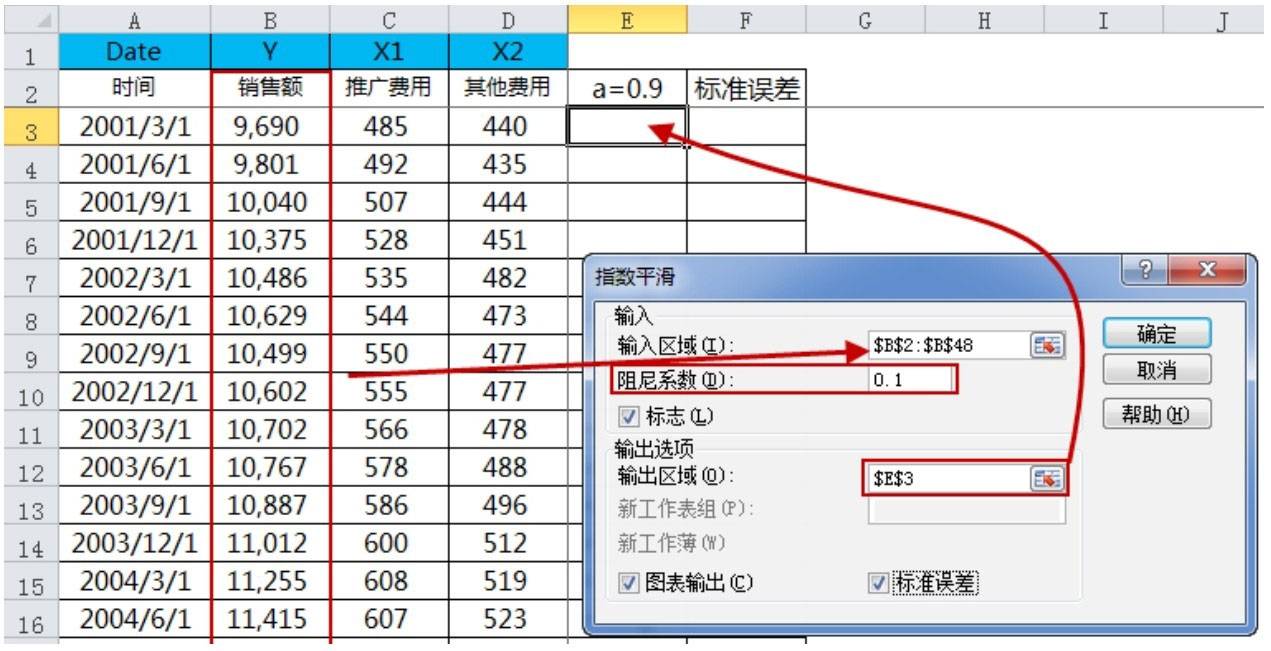
输入
① 输入区域:本例数据源为B2:B48。
② 阻尼系数:阻尼系数(β)=1-平滑系数(α),本例填写阻尼系数= 0.1,意味着平滑系数α=0.9。
③ 标志:本例中勾选【标志】。
输出选项
① 输出区域:本例将结果输出至当前工作表的E3单元格。
② 图表输出:输出由实际数据和指数平滑数据形成的折线图,本例勾选【图表输出】。
③ 标准误差:实际数据与预测数据(指数平滑数据)的标准差,用以显示预测值与实际值的差距,这个数据越小则表明预测数据越准确。
STEP 03 单击【确定】按钮,即可完成。
公式往下拉就可以得到预测结果,如图所示。根据这个图,可以知道2012年第3季度的销售额预测值为15581(E49=0.9*B48+0.1*E48)。
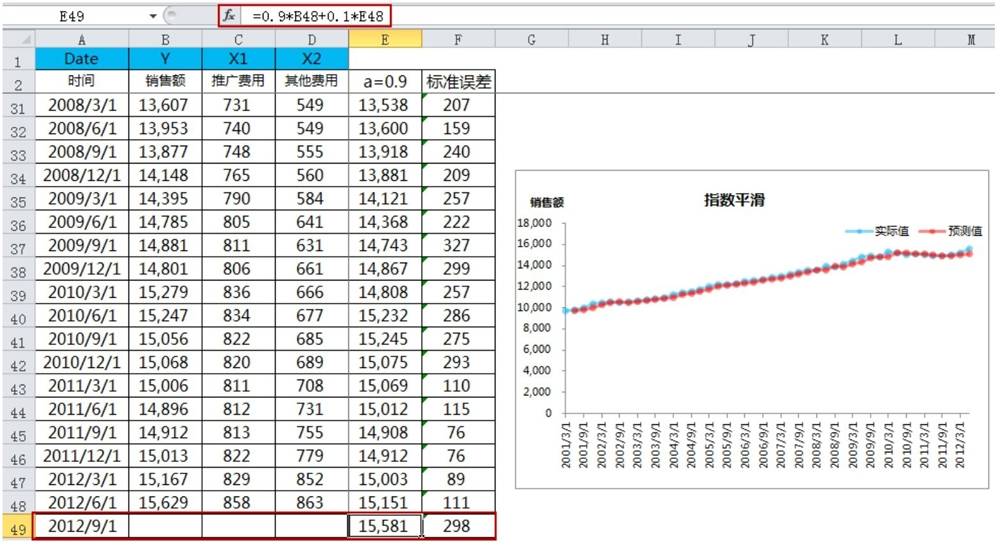
一次指数平滑的预测值=上一期的实际值×平滑系数+上一期的预测值×阻尼系数。
从图可得知,在平滑系数为0.9(即阻尼系数为0.1)时,预测误差最小。
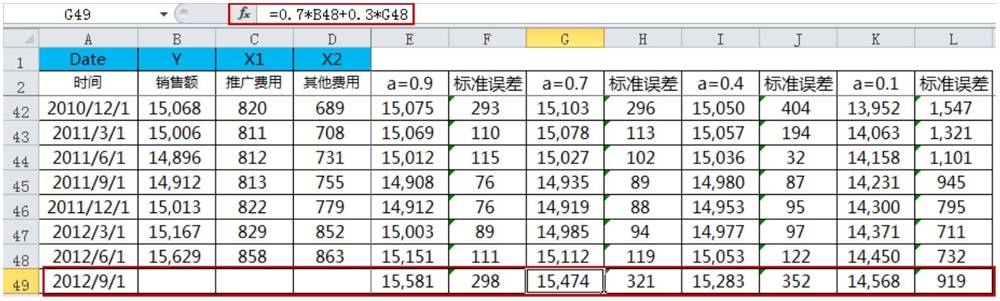
是否使用以上预测结果,最终还要考虑其是否符合业务的实际情况,我们需要辩证地看待问题,不能因为是通过统计方法计算出来的,就直接采用。
同样,二次指数平滑法是建立在一次指数平滑的基础上的,即利用一次指数平滑法得出的预测结果再进行一次平滑。